Example 03 - Generation of a simple, artificial channel impulse response file

The main purpose of SNACS is to simulate GNSS signal propagation in different channels. We start by generating a simple channel impulse response (CIR) file. The CIR will contain a single component that rests at delay = 0 s for the duration of one second and starts to move then. This situation could describe a receiver that is solely receiving the line-of-sight (LOS) signal of a transmitter. After one second it starts to move away from the transmitter.

You can define the maximum speed of the vehicle. The acceleration is computed in a continuous way using the cosine function.

The file is saved in HDF5 format to snacs_cir_moving_los_v01.h5.

This is the corresponging MATLAB script:

%   Example file for
%   
%   SNACS - The Satellite Navigation Radio Channel Simulator
% 
%   Copyright (C) 2010  F. M. Schubert
% 
%   This program is free software: you can redistribute it and/or modify
%   it under the terms of the GNU General Public License as published by
%   the Free Software Foundation, either version 3 of the License, or
%   (at your option) any later version.
% 
%   This program is distributed in the hope that it will be useful,
%   but WITHOUT ANY WARRANTY; without even the implied warranty of
%   MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
%   GNU General Public License for more details.
% 
%   You should have received a copy of the GNU General Public License
%   along with this program.  If not, see <http://www.gnu.org/licenses/>.
% 
% 
%   This file generates an artifical times series with 1 line-of-sight path 
%   that begins to accelerate slowly up to a constant speed.


%% initialization
close all
clear all
clear classes
clc

addpath('../helper_functions');
save_figures = true;

%% parameter setting

h5_filename = 'snacs_cir_moving_los_v01-2.h5';

cir_rate = 500; % Hz
len = 20; % s
cir_amount = len * cir_rate;

speed = 10; % in m/s
start_acceleration = 1.0; % in s
full_speed_at = 3.0; % in s

c0 = 2.99e8; % speed of light in m/s

carrier_frequency = 1.5e9; % in Hz
carrier_wavelength = c0 / carrier_frequency;

%% write Parameters to HDF5 file

simulation_parameters.c0 = c0;
simulation_parameters.cir_rate = cir_rate;
simulation_parameters.cir_amount = cir_amount;

init_snacs_cir_file(h5_filename, simulation_parameters);

%% parameter checks

% TODO check for maximum vehicle speed:
maximum_possible_speed = c0 * cir_rate / carrier_frequency / 2; % sampling theorem

cir_start_acceleration = start_acceleration * cir_rate;
cir_full_speed_at = full_speed_at  * cir_rate;
cirs_acceleration = cir_full_speed_at - cir_start_acceleration;

speeds = zeros(cir_amount, 1);
distances = zeros(cir_amount, 1);
los_complex_amplitudes = zeros(cir_amount, 1);

%% generate channel impulse response

wbh = waitbar(0, 'generating channel impulse response...');

wb_update = cir_amount / 10;

for k = 1:cir_amount
    if (mod(k, wb_update) == 0) waitbar(k/cir_amount, wbh); end;
    
    cir_number = k-1; % k-1: CIR number should start at 0
    
    act_speed = 0;
    
    if (k < cir_start_acceleration)
        % no movement, delay = 0:
        delay = 0;
    elseif ( (k >= cir_start_acceleration) && (k < cir_full_speed_at) )
        % acceleration using a cos function:
        speeds(k) = speed * (cos(pi + (k-cir_start_acceleration) / cirs_acceleration * pi) + 1)/2;

        % linear acceleration:
%         speeds(k) = speed * (k-cir_start_acceleration) / cirs_acceleration;
    elseif (k >= cir_full_speed_at)
        % constant full speed:
        speeds(k) = speed;
    end
    
    % calculate distance using the speed. k * 1/cir_rate is the current
    % time
    distances(k) = speeds(k) * k * 1/cir_rate;
    
    % build struct for writing to HDF5 file:
    los_struct = struct('delay', {0}, 'real', {0}, 'imag', {0});
    
    % calculate the line of sight complex amplitude:
    los_complex_amplitudes(k) = 1.0 * exp(j * (2.0 * pi / carrier_wavelength) * distances(k));

    % calculate LOS delay from distance using speed of light:
    los_struct.delay = distances(k) / c0;
    los_struct.real = real(los_complex_amplitudes(k));
    los_struct.imag = imag(los_complex_amplitudes(k));

    % write this CIR to file:
    append_one_cir_to_cir_file(h5_filename, cir_number, los_struct);
end

close(wbh)

% write reference distances to file:
hdf5write(h5_filename, '/reference_range/range_absolut' , distances, 'WriteMode', 'append');

%% plotting

x_ax = 0:1/cir_rate:cir_amount/cir_rate - 1/cir_rate;

f1 = figure;
title('Receiver Speed');
hold on;
plot(x_ax, speeds);
grid on;
xlabel('Time [s]');
ylabel('Speed [m/s]');
ylim([-10, speed + 20]);

if save_figures save_figure_as_png('../../documentation/doxygen-sources/graphic/example03_receiver-speed.png');  end

figure;
title('Distance Receiver - Transmitter');
hold on;
plot(x_ax, distances);
grid on;
xlabel('Time [s]');
ylabel('Distance [m]');
ylim([-10, distances(end) + 20]);

if save_figures save_figure_as_png('../../documentation/doxygen-sources/graphic/example03_distance.png'); end

figure;
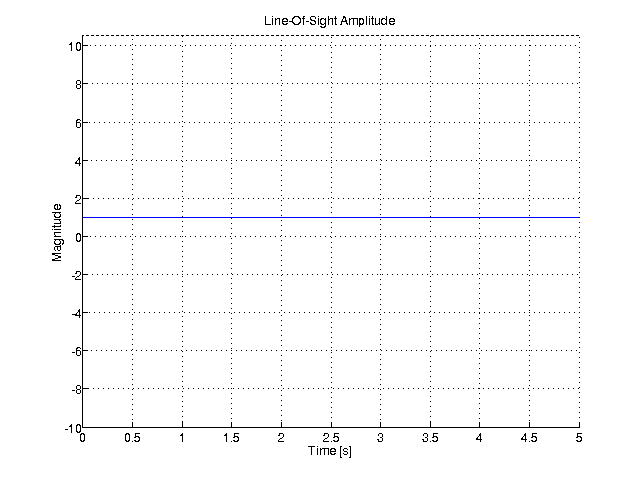
title('Line-Of-Sight Amplitude');
hold on;
plot(x_ax, abs(los_complex_amplitudes));
grid on;
xlabel('Time [s]');
ylabel('Magnitude');
ylim([-10, los_complex_amplitudes(end) + 10]);

if save_figures save_figure_as_png('../../documentation/doxygen-sources/graphic/example03_amplitude.png');  end

figure;
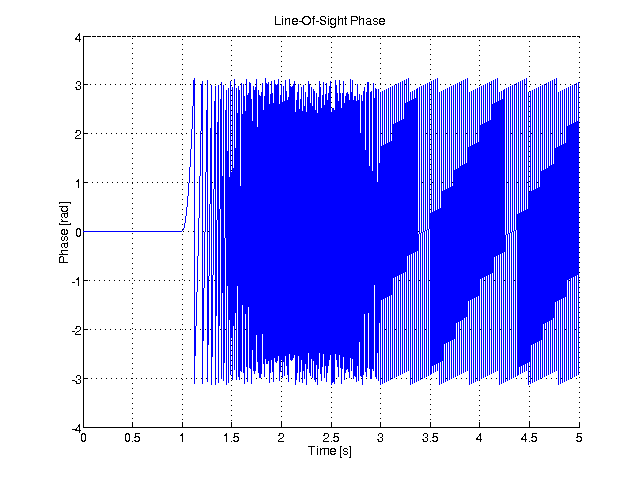
title('Line-Of-Sight Phase');
hold on;
plot(x_ax, angle(los_complex_amplitudes));
grid on;
xlabel('Time [s]');
ylabel('Phase [rad]');
ylim([-4, 4]);

if save_figures save_figure_as_png('../../documentation/doxygen-sources/graphic/example03_phase.png');  end

The output of the MATLAB script:

The resulting receiver speed

The distance receiver - transmitter

The amplitude of the generated CIR

The phase of the generated CIR